monsa
Manual
The following sections briefly describe the method implemented in MONSA, usage in dialog mode as well as the required input and the produced output files.
Introduction
MONSA is an enhanced version of DAMMIN designed for multiphase bead modeling. It enables the simultaneous fitting of multiple datasets, such as those from X-ray or neutron contrast variation experiments.
Running MONSA
MONSA reads in multiple data sets and information about the contrasts and volume fractions of the phases in a particle. The program can simultaneously fit data recorded at different instrumental settings and also with different radiations (e.g. X-rays and neutrons). The structure of the input data is therefore somewhat complicated. The program requires:
- a MASTER file (*.mst) containing the general phase information and references to CONTROL file(s)
- CONTROL file(s) (.con) containing the smearing information for the given setting, information about contrasts and references to DATA files (.dat)
- DATA files (*.dat), containing experimental data at different contrasts
- a seach volume file defining the number of phases and the SEARCH VOLUME for the model
Command-Line Arguments and Options
MONSA recognizes the following command-line options:
| Short Option | Long Option | Description |
|---|---|---|
| --model-format <FMT> | Format of the output models, one of: cif, pdb (default: cif) | |
| -v | --version | Print version information and exit. |
| -h | --help | Print a summary of arguments, options, and exit. |
Interactive Configuration
| Screen Text | Default | Description |
|---|---|---|
| Log file name | N/A | Project identifier, will be used as a prefix for all output file names |
| Project description: | N/A | Free text that will be stored in the log file |
| Master file name: | N/A | Name of the master file |
| Maximum order of harmonics: | 14 | The more harmonics, the more accurate the reconstruction becomes, but the slower the process. May be between 5 and 20 |
| DAM coordinates file name: | N/A | Name of the Search Volume file generated by BODIES. |
| Symmetry: Pn or Pn2 (n=1,2,3,4,5,6): | P1 | Specify the symmetry to enforce on the particle. |
| Reset (unfix) all atoms [Y/N]: | No | If ‘Y’, the phase indices allowed for the atoms in the pdb file are set to. |
| Atomic radius: | var | If the file is prepared by BODIES, the value is read from the file. |
| Atomic volume: | var | Default value is \((4/3)\pi * r^3 / 0.74\) (volume per sphere for dense packing). |
| Preference for non-solvent contacts: | 0.3 | With a value of 0.0, the phase of the atom (solvent or protein) does not influence the looseness penalty weight. When this value is increased, non-solvent contacts are preferred, through the calculation of the looseness penalty weight. If unsure, use the default value. |
| Looseness penalty weight: | 50 | How much the Looseness Penalty shall influence the acceptance or rejection of phase changes. A value of 0.0 disables the penalty. If unsure, use the default value. If unlike smooth surfaces, sharp edges are observed, try decreasing this penalty weight. |
| Discontiguity penalty weight: | 50 | How much the Discontiguity Penalty shall influence the acceptance or rejection of phase changes. A value of 0.0 disables the penalty. If unsure, use the default value. |
| Randomize the initial DAM [Y/N] | Yes | If ‘Y’, the starting model is randomized |
| Fix the overall scale factor [Y/N] | No | If No (recommended), then the overall scale factor, as well as individual relative scale factors for all the data sets will be determined automatically. If the scale factor is known (data on absolute scale) in may be fixed and entered manually. |
| Volume fraction penalty weight | 50 | How much the Volume Fraction Penalty should influence the acceptance or rejection of phase changes. |
| Rg penalty weight | 0.0 | How much the radius of gyration penalty should influence the acceptance or rejection of phase changes. A value of 0.0 disables the penalty. |
| Center penalty weight (negative = WeiPer): | 0.0 | How much the Center Penalty shall influence the acceptance or rejection of phase changes. A value of 0.0 disables the penalty. If unsure, use the default value. |
| Initial annealing temperature : | 10 | If the value is too high, it could take ages for the system to cool down. If the value is too low, the system can be trapped in a local minimum. If unsure use the default value. |
| Annealing schedule factor : | 0.9 | Factor by which the temperature is decreased; 0.95 is a good average value. Faster cooling for smaller systems is possible (0.9), but slower cooling (0.99) needs to be applied more often. |
| Max # of iteration at each T: | var | Finalize temperature step and cool after this many iterations at the latest. |
| Max # of successes at each T: | var | Finalize temperature step and cool after at most this many successful phase changes. |
| Min # of successes to continue: | var | Stop if not at least this many successful state changes within a single temperature step can be done. |
| Number of annealing steps: | 100 | Stop after this number of steps if did not cooled down before. |
| Plot the final fits [Y/N]: | No | Display the final fits. |
Runtime Output
On runtime, two lines of output will be generated for each temperature step:
jAnn: 1 T: 0.100E+02 iSuc: 11718 nEva: 12542 CPU: 0.4056E+02
SqfVal: 22.8539 Rf: 22.25999 Los: 0.1312 Dis: 0.0464 Sca: 0.342E+01
The fields can be interpreted as follows, top-left to bottom-right:
| Field | Description |
|---|---|
| jAnn | Step number. Starts at 1, increases monotonically. |
| T | Temperature measure, starts at an arbitrary high value, decreases each step by the temperature schedule factor |
| iSuc | Number of successful phase changes in this temperature step. The number of successes should slowly decrease, the first couple of steps should be terminated by the maximum number of successes criterion. If instead the maximum number of iterations per step are done, or the number of successes drops suddenly by a large amount, the system should probably be cooled more slowly. |
| nEva | Accumulated number of function evaluations. |
| CPU | Number of seconds since the annealing procedure was started. |
| SqfVal | Goodness of the model (fit + penalties). |
| Rf | Goodness of fit of simulated data versus experimental data, does not take penalties into account. |
| Los | Contribution of Looseness Penalty, not taking the Looseness Penalty Weight into account. |
| Dis | Contribution of Discontiguity Penalty, not taking the Discontiguity Penalty Weight into account. |
| Sca | Scale factor |
MONSA Input Files
Master File
The master file contains general phase information, including volumes, radii of gyration, and connectivity for each phase. The program supports up to four phases. For systems with fewer than four phases, enter zeros for the missing values. The file structure is as follows:
| Line Number | Contents |
|---|---|
| 1 | Title (up to 80 characters) |
| 2 | Four theoretical volumes of each phase in \(\AA^3\) (required) |
| 3 | Four theoretical radius of gyration in \(\AA\) for each phase (optional); use 0.0 if undefined |
| 4 | Connectivity indicator for each phase (required): ‘1’ for ‘interconnected’, ‘0’ for ‘disconnected’, ‘-1’ for ‘symmetry defined’ |
| 5 | Control file name and Npts for Guinier fit (no fit if the corresponding Rg is equal to ‘-1’) |
| 6+ | (Optional) Control file name and Npts for Guinier fit (no fit if the corresponding Rg is equal to ‘-1’) |
Refer to the Example section for a practical demonstration.
Control File
The control file contains the smearing information for the given setting, information about contrasts, and references to the data file. It has the following structure:
Line 1 Resolution file name, resolution setting number (free format)
Line 2 Output file name for the fits (not used) (free format)
Line 3 Title (character*80)
Line 4 Number of points in the setting (free format) (put negative number to indicate nm-1 as angular units)
Line 5 Data file name, contrasts and constants (free format)
etc Erroneous lines skipped; read to the end
The information about the data sets is given in the format:
Filename Dro1 Dro2 Dro3 Dro4 Mult Const Weight
| Field | Description |
|---|---|
| Filename | Filename of the scattering pattern |
| DroN | Contrast of the nth phase. |
| Mult | The scattering pattern is multiplied by this factor after constant subtraction. |
| Const | Constant subtracted to the scattering pattern. |
| Weight | Relative weight of the data set. |
Smearing
If required, MONSA smears the theoretical curves using the resolution function introduced by J. Skov Pedersen et al. (1990), J. Appl. Cryst., 23, 321. Several subroutines for data smearing are provided by J. Skov Pedersen and modified for the use in MONSA.
The resolution file must have the following format (the numbers describe a setting at RISOE SANS instrument):
| Row | Value | Description |
|---|---|---|
| 1 | 0.8 | Effective collimation slit diameter in cm. |
| 2 | 0.35 | Effective sample diameter in cm. |
| 3 | 300 | Collimation distance in cm. |
| 4 | 105 | Sample-detector distance in cm. |
| 5 | 3 | \(\lambda\) in \(\AA\) |
| 6 | 0.18 | \(\sigma(\lambda)/\lambda\) |
| 7 | 1.1 | Pixel size in cm. |
| 8 | 0.0000 | Averaging error (accounted for in Pixel size). |
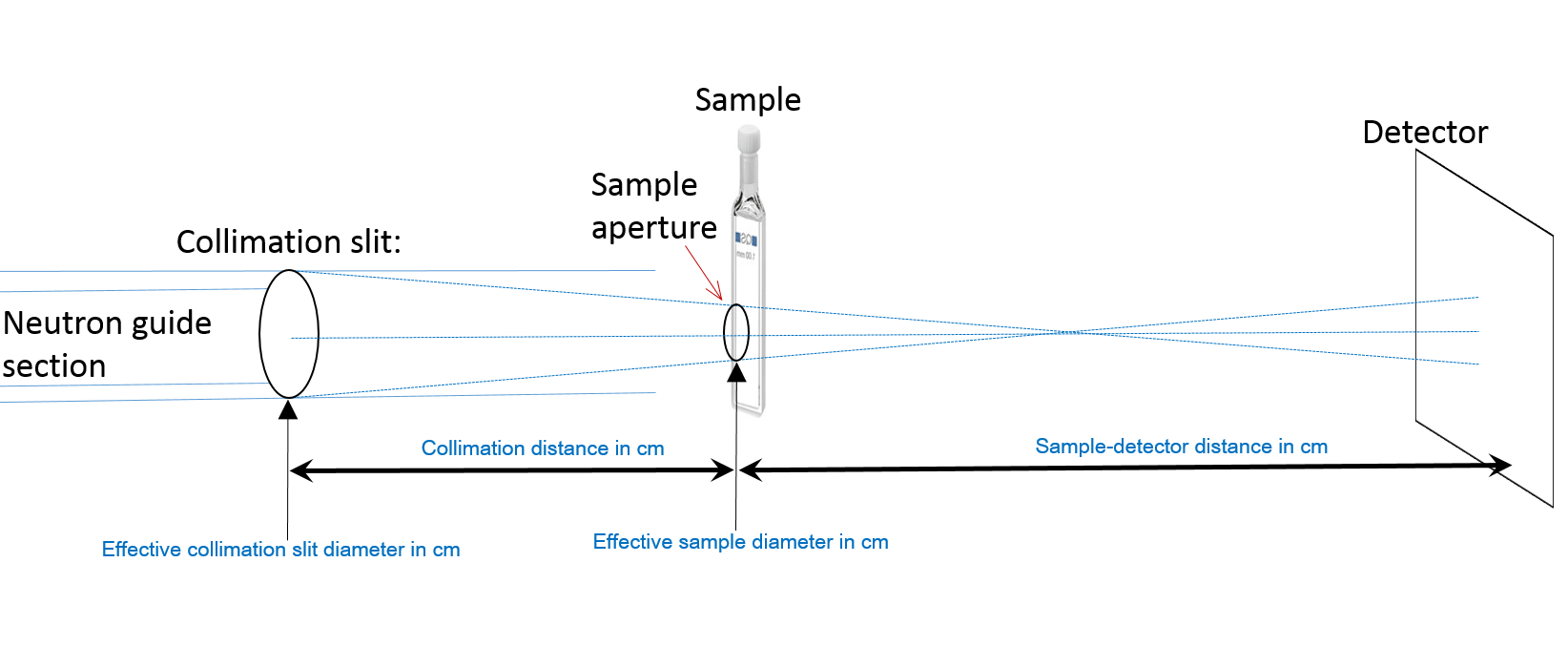
If the file is corrupted or does not exist, no smearing is performed. An example of the resolution file is given below. The resolution setting number is the number of column in the resolution file.
0.00001, 0.00001, 0.00001 , 0.8 , 0.8
0.00001, 0.00001, 0.00001 , 0.30 , 0.35
1100. , 200. , 100. , 300. , 100
180. , 125. , 100. , 110. , 100
6.0 , 5.6 , 1. , 3.22 , 6.
0.10 , 0.09 , 0.01 , 0.18 , 0.18
0.0001 , 1.57 , 0.01 , 1.1 , 1.1
0.0000 , 0.0000 , 0.0000 , 0.0000 , 0.0000
Data Files
MONSA requires background-subtracted experimental SAS data (.dat).
Search Volume File
MONSA requires a search volume file as generated by BODIES for the given number of phases and given number of dummy atoms. In a general case, one can always use the spherical search volume with the diameter equal to Dmax, as in DAMMIN. MONSA will automatically calculate the number of phases in the search model when reading this file. The number of dummy atoms in the search volume must not exceed 10000.
To note: in previous releases two helper applications, DAMESV and DAMEMB, were included to generate suitable search volumes for MONSA. The functionality of both applications was integrated into the search-volume mode of BODIES.
MONSA Output Files
With each successful run, MONSA creates a set of output files, each filename starts with a customizable prefix that gets an extension appended. If a prefix has been used before, existing files will be overwritten without further note.
| Extension | Description |
|---|---|
| .log | Contains the same information as the screen output and is updated during execution of the program. |
| -i.pdb or -i.cif | Current model of the ith phase in either .pdb or .cif format, depending on model-format option. The comments section of the file contains information about the application used and about the parameters of the model, e.g. penalties and goodness-of-fit to the data \((\chi^2)\). |
| -i.fit | Fit of the simulated scattering curve versus the real-data; i refers to the respective data file. |
Example
Master file for the test example: contrast variation simulated data of a 30S ribosomal subunit-like particle consisting of “RNA” (phase 2, density = 4.0) with some “proteins” inside (phase 1; density = 2.0)
Master file for quazi-30S model randomized data to s=0.2
3.7e5 8.7e5 0.00 0.0 ! Desired Volumes
49.0 61.0 0.00 0.0 ! Desired Rgs
0 1 0 0 ! Connectivity
'test.con' 10 ! Control file name; Rgs will be
! computed from 10 first points
Control file for the test example
'Point collimation' 1 !! No smearing
'test.fit' !! Output fits
Test for 30S -- use randomized data up to 0.2 !! Title
98 !! Number of points
'0r1.dat' 2.00 4.00 0.00 0.00 1.000 0.0 1.00 0
'2r1.dat' 0.00 2.00 0.00 0.00 1.000 0.0 1.00 0
'4r1.dat' -2.00 0.00 0.00 0.00 1.000 0.0 1.00 0
'6r1.dat' -4.00 -2.00 0.00 0.00 1.000 0.0 1.00 0
'infr1.dat' 1.00 1.00 0.00 0.00 1.e-6 0.0 1.00 0
Here, the data sets ‘?r1.dat’ correspond to the scattering patterns from the test body in solvents with density 0.0, 2.0, 4.0, 6.0. The set ‘infr1.dat’ corresponds to “shape scattering” (infinite contrast). Note that the test would have worked also without the ‘infinite contrast’ data. Please note:
- filename should be given in quotes
- put zeroes as contrasts for phases, which are not present;
- all files in the setting MUST have the same number of points and the same angular axis; if you have data set(s) on another angular grid(s), put them as another setting(s);
- from each data set, a constant “Const” will be subtracted and the result will be multiplied by “Mult”;
- the data sets will be weighted with the relative weight “Weight” in the total discrepancy; reducing the weight is equivalent to increasing errors in the data file;
- number of points must not exceed 2048. Choose the value, so that the maximal s value becomes \(2.5 \text{nm}^{-1}\).
After the configuration, the program computes the parameters for the initial state and the simulated annealing procedure starts:
--- Starting values ---
Total scale factor : 3.51404919007708
Function value : 733.688635068192
Overall discrepancy : 696.618264908644
SQRT(Overall discr.) : 26.3935269509144
DAM looseness : 0.137137795235494
DAM discontiguity : 6.681519817391703E-002
Overall penalty : 37.0703701595471
jAnn: 1 T: 0.100E+02 iSuc: 11718 nEva: 12513 CPU: 0.4555E+02
SqfVal: 23.3509 Rf: 22.69190 Los: 0.1314 Dis: 0.0517 Sca: 0.338E+01
jAnn: 2 T: 0.900E+01 iSuc: 11718 nEva: 25119 CPU: 0.9059E+02
SqfVal: 22.7818 Rf: 22.15299 Los: 0.1243 Dis: 0.0272 Sca: 0.341E+01
jAnn: 3 T: 0.810E+01 iSuc: 11718 nEva: 37867 CPU: 0.1366E+03
SqfVal: 22.5775 Rf: 22.01942 Los: 0.1295 Dis: 0.0268 Sca: 0.327E+01
jAnn: 4 T: 0.729E+01 iSuc: 11718 nEva: 50732 CPU: 0.1830E+03
SqfVal: 22.5775 Rf: 22.01942 Los: 0.1295 Dis: 0.0268 Sca: 0.327E+01
jAnn: 5 T: 0.656E+01 iSuc: 11718 nEva: 63648 CPU: 0.2309E+03
SqfVal: 22.5775 Rf: 22.01942 Los: 0.1295 Dis: 0.0268 Sca: 0.327E+01
jAnn: 6 T: 0.590E+01 iSuc: 11718 nEva: 76727 CPU: 0.2778E+03
SqfVal: 22.3977 Rf: 21.72769 Los: 0.1368 Dis: 0.0467 Sca: 0.330E+01
jAnn: 7 T: 0.531E+01 iSuc: 11718 nEva: 89852 CPU: 0.3235E+03
SqfVal: 22.2560 Rf: 21.66409 Los: 0.1292 Dis: 0.0197 Sca: 0.329E+01
jAnn: 8 T: 0.478E+01 iSuc: 11718 nEva: 103078 CPU: 0.3704E+03
SqfVal: 21.9930 Rf: 21